Microstructural Magnetic Modelling of Magnetic Anisotropy Considering Crystallographic Texture by Dr Jun Liu

A paradox regarding tensor permeability approaches for considering texture effects on magnetic anisotropy is solved. That is, a magnetic permeability tensor satisfying all the cubic crystal symmetries of steels must reduce to a scalar hence would give isotropic magnetic properties, which would be inconsistent with the experimentally observed anisotropy.

This is the first time both the microstructure and crystallographic texture have been considered in predictions of magnetic anisotropy.

Magnetic anisotropy

Anisotropy is a fairly common phenomenon in magnetic alloys such that the properties of a material vary with directions along which they are measured. This can be a desirable or an unwanted phenomenon. On one hand, some soft magnetic alloys and steel products, e.g. grain orientated electrical steels and deep drawing steel grades, are tailored for specific applications to take advantages of the superior properties along favoured directions. On the other, unwanted anisotropy, e.g., in non-grain-orientated electrical steels and hot rolled plate, can impair product quality and uniformity and, more often than not, is unavoidable. In either case, it is imperative to be able to predict the magnetic anisotropy in magnetic alloys given the microstructural anisotropy in the alloys.

The power of averaging

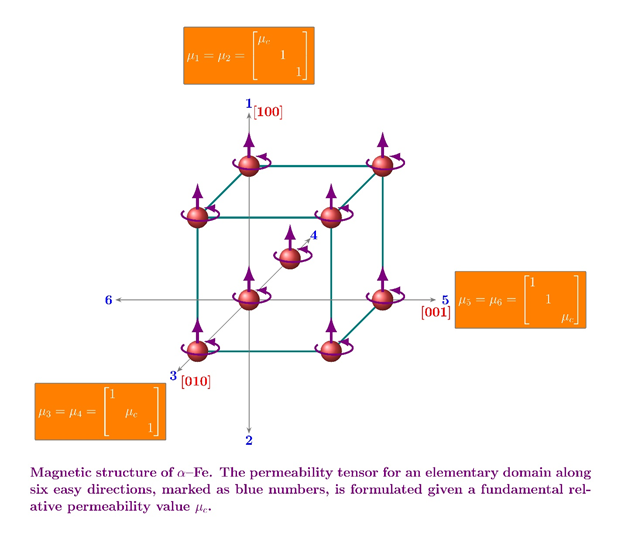
Iron and steel crystal structures are magnetically anisotropic due to the alignment of magnetic dipoles in a crystal cell [1], as schematically illustrated in the figure. It has also been experimentally confirmed that the cube edges (〈100〉) and the cube diagonals (〈111〉) are the easiest and the hardest directions of magnetising respectively in iron [2] and silicon-iron [3] single crystals. This fundamental magnetic anisotropy is inherited by each grain (a single crystal in certain orientation) in polycrystalline steels. If grains are randomly orientated, the anisotropy effect averages out and, as a result, the steels exhibit isotropic behaviours. If there are preferred crystallographic orientations present, often referred to as crystallographic texture, the overall average properties have a certain anisotropy associated with the texture. This simple yet useful averaging approach has been widely applied to predict mechanical anisotropy of polycrystalline materials, e.g. elastic modulus, based on the corresponding single crystal properties.

The paradox

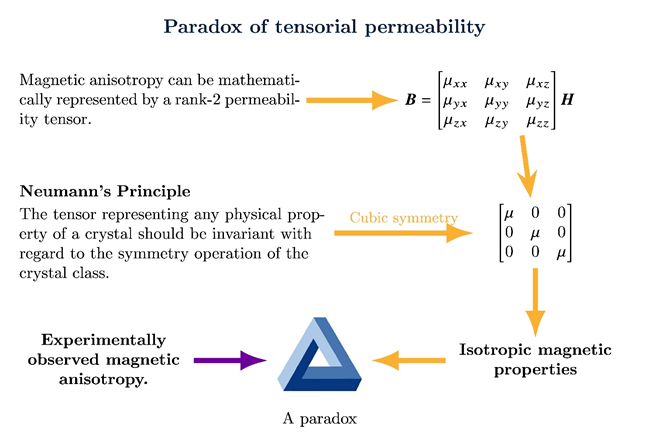
One could potentially apply this approach to magnetic anisotropy. However, a paradox regarding the permeability tensor—an intrinsic material property and magnetic counterpart of the mechanical property, elasticity tensor—is in the way as illustrated in the diagram below. Unlike the elasticity tensor, the permeability tensor is of lower rank, that is, has fewer independent elements. According to the Neumann’s principle, the tensor representing any physical property of a crystal should be invariant with regard to the symmetry operation of the crystal class. That is, some of the elements in the tensor must be zero; some must be equal to each another. In the case of cubic crystals such as iron or steel, the permeability tensor that satisfies all the symmetries must reduce to a scalar, a single value. It follows that the corresponding magnetic properties should be isotropic, which would be inconsistent with experiments. This paradox rendered the tensorial approach inapplicable as far as the cubic crystallographic texture is concerned and thereby make people resort to empirical approaches as a partial solution or way around.

The fundamental reason is that the magnetic structure of iron or steels does not have all the symmetries of the crystal structure. Magnetic domains exist in ferromagnetic materials; there are more than one direction of magnetic domains even in a single crystal. Their magnetic structure has a lower symmetry than the crystal structure itself does as illustrated in the figure due to the directionality of the magnetic spin. We have solved this paradox by formulating the fundamental permeability tensor at the magnetic domain level without violating the general Neumann’s principle and then extend it to single crystals and then polycrystalline grains in turn. Thus, the aforementioned averaging approach based on single elementary domain properties can be used to predict polycrystalline ones using the tensor approach.

Our solution

The permeability tensors for elementary domains are formulated based on some simple assumptions that are consistent with the widely accepted domain theories. The statistical domain configuration, that is, how many of them orientate along each of the six easy directions, were already solved in 1930s [4] but rarely applied by others. The single crystal permeability tensor in its own crystal structure reference frame (i.e., consisting of three easy directions along the x, y and z axis respectively), is just the average over all elementary domains of a configuration that depends on the applied field and the magnetisation of the material. The permeability tensor for polycrystalline steels, in the specimen reference frame, can then be formulated by rotating the tensor. The rotation matrix is given by the crystallographic orientations of the grains, which can be obtained by, say, electron backscatter diffraction (EBSD) and used as input to the model. We have also considered the grain boundaries as the elementary domains that do not orientate along any easy directions. These grain-boundary elementary domains have been treated as a loss of elementary domains for simplification. This way the grain size effects can also be considered based on magnetic domain theories. Now that one has the permeability tensors of each grain in polycrystalline steels as a function of the crystallographic orientations of the grains; one can take the above averaging approach to find the anisotropic magnetic permeability of the polycrystalline microstructure. We have done the averaging in a finite element (FE) model.

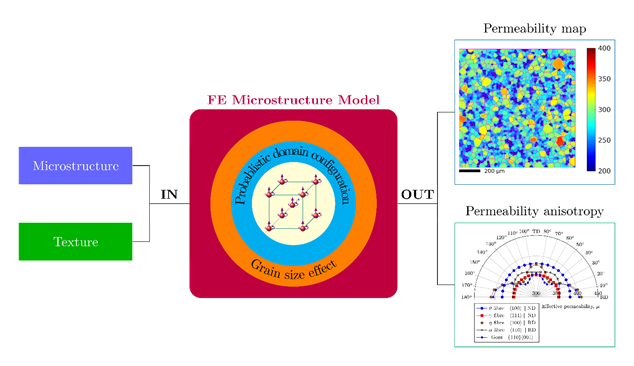
Capability of the model

The present finite element microstructure model, as illustrated in the figure below, can predict consistent and logical effective permeability behaviours and the angle between B (magnetisation) and H (magnetic field) for some selected typical textures that are important and common in steel manufacturing. The model has proved capable of capturing the crystallographic texture, the grain size and the applied field effects on the magnetic anisotropy of steels based on the magnetic domain theory. The predicted effective permeability curves as a function of the magnetic field directions and the permeability maps can serve as a quantitative characterisation of the magnetic anisotropy as well as an enhanced visual indication of the crystallographic texture from magnetic values. These capabilities have been initially validated against a commercial grain oriented electrical steels featuring strong Goss texture and magnetic anisotropy.

Potential applications

The present model is anticipated to be used

• To provide the permeability anisotropy for predicting sensor measurements for low field electromagnetic sensors used for monitoring steel quality during processing and / or for the interpreting the EM sensor signals to infer the texture of the steel.
• To predict anisotropic effective permeability values that can be input into other macroscopic FE electromagnetic models as the material property, say, the permeability of electrical steel components of an electric motor, to consider the steel’s microstructure and texture.
• To be coupled with other microstructural models, e.g., the microstructure-based crystal plasticity models, for multi-physics modelling.

The work has been published on Philosophical Magazine and available online in March 2021 [5].

References

[1]       R. E. Newnham, “Magnetic phenomena,” in Properties of materials : anisotropy, symmetry, structure, Oxford University Press, 2005, pp. 122–146.

[2]       K. Honda, S. Kaya, and Y. Masuyama, “On the Magnetic Properties of Single Crystals of Iron,” Nature, vol. 117, no. 2952, pp. 753–754, May 1926, doi: 10.1038/117753a0.

[3]       H. J. Williams, “Magnetic Properties of Single Crystals of Silicon Iron,” Phys. Rev., vol. 52, no. 7, pp. 747–751, Oct. 1937, doi: 10.1103/PhysRev.52.747.

[4]       R. M. Bozorth, “The Theory of the Ferromagnetic Anisotropy of Single Crystals,” Phys. Rev., vol. 42, no. 6, pp. 882–892, Dec. 1932, doi: 10.1103/PhysRev.42.882.

[5]       J. Liu and C. Davis, “Tensorial permeability microstructure model considering crystallographic texture and grain size for evaluation of magnetic anisotropy in polycrystalline steels,” Philos. Mag., vol. 101, no. 10, pp. 1224–1244, May 2021, doi: 10.1080/14786435.2021.1892229.