Nature’s most luminous objects?

For instance, the radiation emitted during the final second before the two black holes merge could be 5% of the total mass of the system. This makes black hole binaries emit in gravitational waves more energy than a star of comparable mass emits in optical radiation throughout its billions of years of life-time. Black hole binaries could well be Nature’s most luminous objects!

Chirps and ringdowns

Gravitational waves from a binary are predominantly emitted at twice the orbital frequency and carry away the binary’s energy and angular momentum. Since the system loses its rotational energy, the two black holes gradually inspiral towards each other. Black holes that are closer together emit more radiation, thereby accelerating the inspiral. This produces a characteristic chirp waveform whose amplitude and frequency both increase with time until eventually the two bodies merge together. Prior to merger, the two black holes approach each other at speeds very close to that of light; their collision will be astounding.

The merger will result in a highly deformed single black hole which rids itself of its deformity by emitting gravitational radiation that is characteristic of the mass and spin of the final black hole. This is called the quasi-normal mode or the ring down signal. Laser interferometric detectors, such as LIGO, GEO600 and Virgo, should be able to detect the waves from the last few minutes of the binary’s evolution. The ring-down signal is not unlike the radiation from a bell that is stuck with a hammer except that black holes are far more simple objects than a bell and the frequency and damping time of the radiation depends only on the final black hole’s mass and spin.

The last three minutes

Gravitational astronomy is expected to resovle a puzzle that has gripped astronomers for half a century. Gamma-ray bursts are extremely luminous events that were serendipetously discovered by US spy sattelites in the 1960’s. In a matter of a few seconds the source outputs more energy than a star does in its entire life-time. The origin of gamma-ray bursts is still not known but astronomers suspect that they are the aftermath of the merger of neutron stars in a binary system. Some gamma-ray bursts could be from the merger of a neutron star and a black hole. Resolving this puzzle has remained a principle theme of theoretical astrophysics.

We already know that binary neutron stars are a common occurrance in our own galaxy. We also know that some of them would coalesce within the next 100-300 million years. Extrapolating to the distant Universe, one expects coalescence of binary neturon stars to be common place, occuring about once a day. LIGO, GEO600 and Virgo detectors are sensitive enough to observe the slow inspiral of a binary neutron star during the final few minutes of its life for sources within 50 million light years (initial detectors) to 500 million light years (advanced detectors).

We do not much about mixed binaries consisting of a neutron star and a black hole. Advanced gravitational detectors that are expected to be operating by 2015 should reveal such systems and solve the gamma-ray burst puzzle.

Standard sirens

Binary black holes are an astronomer’s standard candles or, more appropriately, standard sirens. Cardiff physicist Bernard Schutz was the first realize this property of black hole binaries.

No two stars are alike. Two stars with exactly the same mass are bound to look very different from each other. In fact, the composition of a star is what makes it different from every other star. Black holes, however, completely hide what they are made up of. Therefore, gravitational radiation that is emitted during the slow inspiral of a black hole binary depends only on the masses of the two black holes.

Just as optical radiation and radio waves, the luminosity of gravitational radiation falls off in inverse proportion to the square of the distance from the source. This makes binary black hole inspirals standard sirens: if we know what the masses of the two black holes are then we can infer the distance to the source by measuring its apparent luminosity. We can precisely measure the masses because the rate at which the frequency and amplitude of an inspiral increases depends only on the masses.

A new tool for precision cosmology

Cosmology is like map making. To make a good map, you need to measure distances to various objects very precisely. In the case of the Universe, map making is a bit more complicated because the objects in it are not at the same spot because of Universe’s expansion. Therefore, for precision cosmology one needs two tools: a tool to measure distances, and another to measure the expansion rate.

Gravitational astronomy naturally provides a tool for measuring distances accurately. Electromagnetic astronomy, via spectroscopy, can measure the expansion rate very precisely. Thus, two astronomies working in harmony will give us unprecedented insights into the nature of the Universe including its dark contents such as dark matter and dark energy.

Merger waveforms

The last stages in the evolution of a black hole binary is dominated by relativistic motion and strong gravitational fields. Although most of the evolution of a binary black hole can be understood using approximate methods, the description of the final merger phase requires an accurate solution to the non-linear equations of general relativity, which can only be solved using sophisticated analytical and numerical methods.

Buonanno and Damour were the first to make a breakthrough, their so-called Effective One-Body (EOB) formalism provided a way of deriving the merger part of the waveform. The full numerical solution was obtained by Pretorius in 2005 paving the way for a detailed study of the merger problem. The numerical solutions vindicated the EOB predictions that the transition from inpsiral to merger and the final ring down of the resulting single black hole is pretty smooth in spite of the non-linearities.

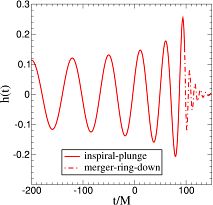
The waveform as predicted by analytical approach of Buonanno and Damour to the binary black hole problem.

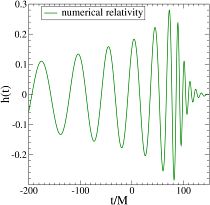
The waveform from Numerical simulations by Pretorius.

The numerical simulation of the merger event, a still image of which is at the top, helps Cardiff researchers to search for binary black holes in data from interferometric gravitational wave detectors.

Movie of numerical simulation [15.9 MB]

For instance, the waveforms shown in the plots above give us the inspiral, merger and ring down phases of the binary evolution. Before full numerical solutions to Einstein’s equations were possible, we used only the inspiral and the ring down parts of the waveform separately to search for binary black holes. The availability of these solutions will help us to increase the reach of interferometers to a far greater distance than was possible before.

Observing Black Hole Collisions

The detailed knowledge of the detected signal will allow us to infer the masses and spins of the binary components and its orientation in space. The knowledge so gained will enable strong field tests of general relativity such as the no-hair theorem which states that the geometry of a black hole is entirely determined by its mass and spin. Additionally, it will be a new observational tool to map and measure the Universe. For instance, being standard candles binary black holes will make it possible to measure the luminosity distance to sources at cosmological distances thereby providing a new tool for cosmology. In particular, Cardiff relativists have shown that by observing many such binaries at cosmological distances, it will be possible to measure the mean density of the Universe and its expansion rate very accurately. LISA observations of binary black holes will also help in measuring the dark energy equation of state (see the Section on super-massive black holes).